Heb jij je dat ook wel eens afgevraagd?
Waarom je bij keersommen wel mag omdraaien
en bij het delen niet?
Het heeft te maken met de getalfamilies
van keersommmen.
De getallen 3, 4 horen bij de 12.
Of je nou 3 groepjes van 4 hebt
of 4 groepjes van 3,
samen is het 12.
Kijk als je de verdeling naast elkaar zet
zie je het heel goed.
Of je nou vier groepjes van drie maakt.
Of dat je drie groepjes van vier maakt.
Het blijft samen 12.
Dat is waarom je de getallen mag omdraaien.
Wil je precies weten of het wel of niet kan?
Haal dan de getalfamilie erbij.
De keersommen die bij de getalfamilie horen.
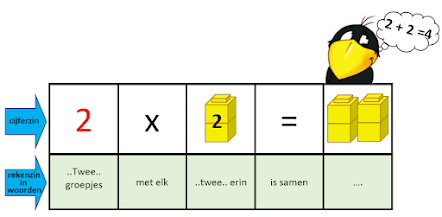
Schrijven we op in cijferzinnen.
We noemen dat rekenzinnen.
Rekenzinnen vertellen je wat er gebeurt is.
Het kan uit een cijferzin bestaan...
dat noemen we een som.
Het kan ook uit woorden bestaan.
Dat noemen we een verhaaltjes som.
Het is handig dat we rekenzinnen hebben.
We gebruiken cijfers en tekens om
zo weinig mogelijk op te hoeven schrijven,
terwijl we toch weten wat er wordt bedoelt.
Kijk maar.....
Bij het plaatje 3 groepjes van 4
horen de rekenzinnen:
Maar als je andere groepjes maakt van 12
krijg je andere rekenzinnen:
hoort bij:
Onthoud dus goed dat cijferzinnen die
bij elkaar horen, tot dezelfde getalfamilie horen.
Kijk, hier zie je cijferzinnen
die bij elkaar horen nog een keertje.
Wist je trouwens dat bij de twee keersommen
van een getalfamilie
ook twee deelsommen horen?
Dat is super handig om te weten!
Dit weten noemen we rekeninzicht.
Het is een belangrijk woord.
Oh ja....
Wat de geheime code van de deelsommen
precies betekenen, vertel ik in een ander blog.
